Photon Bose-Einstein-Condensates:
Statistical Physics
What is a Bose-Einstein condensate?
Bose-Einstein condensation, the macroscopic ground state occupation of a system of bosonic particles below a critical temperature, was observed for an atomic gas first in 1995. Photons, the quantized particles of light, usually exibit no Bose-Einstein condensation, because for Planck's blackbody radiation the particle number is not conserved and the photons disappear at low temperature in the walls of the system. We investigate the thermodynamics of a two-dimensional photon gas in a dye-molecule filled optical microresonator. The resonator mirrors here provide both a confining trapping potential as well as a nonvanishing effective mass of the photon, so that the system is formally equivalent to harmonically confined two-dimensional gas of massive particles. By repeated absorption and emission processes in dye molecules, the photon gas thermalizes with the temperature of the dye solution, which is at room temperature. The so far observed properties of the photon Bose-Einstein condensate (photon BEC) in many respects resemble those of atomic Bose-Einstein condensates, while the 10 order of magnitude smaller effective photon mass allows for transiton temperatures at room temperature.
We have determined the particle number statistics of the photon condensate generated in the dye microresonator system. For small photon numbers, for condensed state conditions unusually high values of the normalized intensity correlation of up to g(2)(0)=1.7 are observed, which significantly differs from the for usual Bose-Einstein-condensates or also lasers observed value g(2)(0)=1. The background of the enhanced particle number fluctuations is that the photon condensate can effectively exchange particles with the photo-excitable dye molecules, as can be well described in the picture of the grand canonical statistical ensemble. The measurements provide direct evidence for a grand canonical Bose-Einstein condensate. For high condensate particle numbers, or also for small molecular numbers, again the usual value g(2)(0)=1 is observed, which then corresponds to a canonical ensemble.
In other works, we have determined the heat capacity of condensed light. Along this line, we investigate different effects related to statistical mechanics.
J. Klaers, J. Schmitt, F. Vewinger, and M. Weitz, Phys. Unserer Zeit 42, 58 (2011)
J. Klaers and M. Weitz, in Novel Superfluids, Vol. 1, K. H. Bennemann and J. B. Ketterson (Eds.) (Oxford University Press, Oxford, 2013), arXiv: 1210.7707
E. Busley, L. Espert Miranda, M. Weitz, and J. Schmitt, Phys. in unserer Zeit 53, 166 (2022)

Close-Up of the microcavity setup to observe a photon BEC. A drop of dye solution is located between two highly reflecting mirrors, visible from the bright yellow/red fluorescence in the center. The pump lights enters the cavity via the prisms on the backside of the mirrors.
Photons in Box Potentials
In this project, we study the statistical physics of photon condensates in box potentials. In a box, one can have a macroscopic occupation of the ground state, without undergoing a phase transition, i.e no discontinuity in a thermodynamic quantity like the specific heat. As the system is homogeneous, one can extract mechanical properties such as the compressibility.

Artist's view of photons in a box
Fluctuating Photon Gas
The fluctuation-dissipation relation is a cornerstone of statistical physics, relating fluctuation properties of equilibrium properties such as the compressibility.

The photon gas in the microresonator shows unusual fluctuation properties, indicated by the "grainy structure" of the gas. For large reservoirs, the fluctuations become stronger than usual, and the fluctuations can become as large as the average photon number.
Photon Gases in One Dimension
When looking at quantum gases, one and two dimensions are clearly distinct. In two dimensions, one expects a true phase transition for a harmonically trapped gas, while in one dimension a trapping potential stronger than linear is requried. In this project, we study the transition from 1D to 2D using polymer-based microstructures on top of one of the mirrors to trap the photon gas.
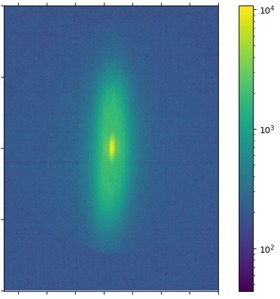
Emission from a microstructured potential, the vertical axis corresponds to approxiamtely 100 µm,
Key publications:
J. Klaers, J. Schmitt, F. Vewinger, and M. Weitz, Nature 468, 545 (2010).
J. Schmitt, T. Damm, D. Dung, F. Vewinger, J. Klaers, and M. Weitz, Phys. Rev. Lett. 112, 030401 (2014)
E. Busley, L. Espert Miranda, A. Redmann, C. Kurtscheid, K. Karkihalli Umesh, F. Vewinger, M. Weitz, J. Schmitt, Science 375, 6587 (2022)
F. E. Öztürk, T. Lappe, G. Hellmann, J. Schmitt, J. Klaers, F. Vewinger, J. Kroha, M. Weitz, Science 372, 6537 (2021)
