Bose-Einstein-Condensates of Photons in Variable Potentials
Trapping light in lattice structures
In a dye-filled microcavity, where Bose-Einstein condensation of light has been firstly observed, the two-dimensional trapping potential for the photonic gas is given by the resonator geometry. Transversally varying mirror distances and curvatures yield a locally varying potential landscape. Locally increased mirror distances act as an attractive potential as photons require less energies (larger wavelenghts) to fulfill the confinement conditions.
We have elaborated experimental techniques with which we can alter the microcavity geometry such that lattice potentials for photons can be realized. In a first approach the physical distance between resonator mirrors was unchanged and the the refractive index of the dye solution, to which a thermosensitive polymer was added, was temporarily increased via spatially selective heating. The resulting elongation of the optical path yields local potential minima which we were able to arrange in varying lattice structures.
In other work, we have developed a technique for the permanent structuring of in principle arbitrarily shaped potentials for cavity photons. For this, the reflecting surface of dielectric mirrors is spatially structured by controlled heat-induced delamination. The local heating is achieved through irradiation with a focused, transversally steerable laser beam, which leads to heating from absorption in a thin silicon layer placed below one of the cavity mirrors reflecting dielectric coatings. The spatial surface reflecting surface structuring seemingly does not noticeably affect the mirror reflectivity.
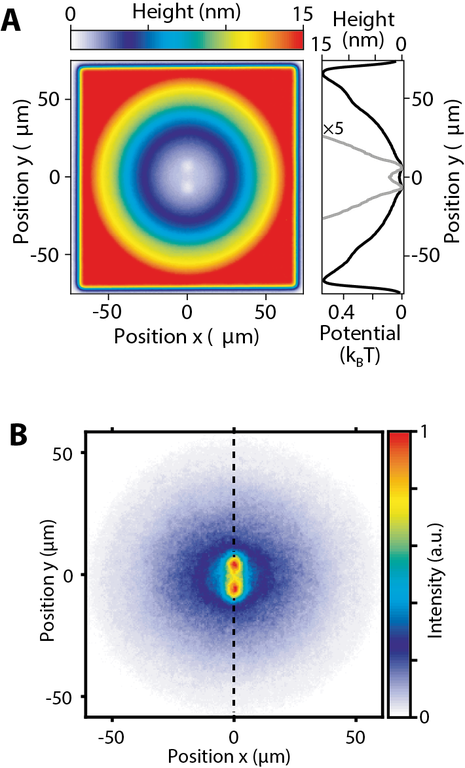
The permanent structuring method has recently enabled us to demonstrate Bose-Einstein condensation into a coherently split state of light. For this, in the dye microcavity environment we create a double-well potential that is superimposed by a harmonic trap potential. Photons thermalize to room temperature in the combined trap by repeated absorption-reemission processes on the dye molecules. Bose-Einstein condensation here leads to a macroscopic population of photons in the symmetric linear combination of the eigenfunctions localized in the two sites, which is the system ground state in the cavity. We have also verified the phase coherence between the optical wavefunction components of the different sites. More recently, also more complex potential structures have been successfully realized using the permanent structuring method, as coupled arrays with a larger number of sites.
Condensation into a coherent superposition
A, Surface profile of a delaminated resonator mirror (left) and resulting potential in the microcavity (right). B, Spatial photon distribution above the condensation threshold. The macroscopic occupation of the symmetric superposition ground state in the trap center is clearly visible.

Artist's view of the coherently split condensate of light.
D. Dung, C. Kurtscheid, T. Damm, J. Schmitt, F. Vewinger, M. Weitz, and J. Klaers, Nature Photonics 11, 565 (2017).
C. Kurtscheid, D. Dung, E. Busley, F. Vewinger, A. Rosch, and M. Weitz, Science 366, 894 (2019).
C. Kurtscheid, D. Dung, A. Redmann, E. Busley, J. Klaers, F. Vewinger, J. Schmitt, and M. Weitz, Europhys. Lett. 130, 54001 (2020).
